Motivation

I took some classes in school where I learned topics of aerodynamics and numerical integration methods, and I enjoy playing golf, but until now I never got the satisfaction of studying the aerodynamics of a golf ball. Thus, I dug through a few research papers out of curiosity, and I found the paper referenced here to be pretty digestible for such a complex topic.

Lyu, Bin, et al. "Aerodynamics of Golf Balls in Still Air." Proceedings of the 12th Conference of the International Sports Engineering Association, 26-29 March 2018, Brisbane, Queensland, Australia, 23 February 2018

Aerodynamic Equations

It's important that we list some of the variables we will be referencing

Variables

• Re - Reynold's Number
• V - magnitude of the velocity vector
• ρ - air density
• ν - kinematic viscosity of air
• g - gravity (-9.81 m/s)
• m - mass of a golf ball 0.0459 kg
• A - cross sectional area of a golf ball
• D - diameter of a golf ball
• a - acceleration
• S - non-dimensional spin factor
• C_L - lift coefficient
• C_D - drag coefficient
• F_L - force due to lift
• F_D - force due to drag

Defining Equations

Reynold's Number

The Reynold's number can be thought of as the ratio of inertial forces to viscous forces. As we can see from the equation, this number is directly proportional to ball diameter and velocity and inversely related to kinematic viscosity of the air.

$$\text{Re} = \frac{{VD}}{{\nu}}$$

The Reynold's number is important as the study we are leveraging to find the lift and drag coefficients are defined in terms of the ball Reynold's number.

Non-dimensional Spin Factor

The non-dimensional spin factor is a parameter that reflects how much lift our ball is able to generate as a function of it's radius, the spin rate, and velocity.

$$S = \frac{{\omega r}}{{V}}$$

Lift and Drag Coefficients

The lift and drag coefficients are fundamental equations in the study of aerodynamics

$$C_D = \frac{{2 F_D}}{{\rho V^2 A}}$$ $$C_L = \frac{{2 F_L}}{{\rho V^2 A}}$$

Compute Ball Acceleration from Lift & Drag Coefficients

Ultimately, our goal here is to compute the golf ball acceleration at each point in time so we can then use our numerical integration methods to calculate velocity and position.

Let's compute acceleration from the general equations for lift and drag coefficients.

$$C_D = \frac{{2 F_D}}{{\rho V^2 A}}$$ $$C_L = \frac{{2 F_L}}{{\rho V^2 A}}$$

Rewriting these equations to solve for Force (F):

$$F_D = \frac{{1}}{{2}} {{\rho V^2 A C_D}}$$ $$F_L = \frac{{1}}{{2}} {{\rho V^2 A C_L}}$$

Now, we can use Newton's 2nd Law of Motion (F = ma) to solve for acceleration in both of these equations

$$a_D = \frac{{\rho V^2 A C_D}}{{2 m}}$$ $$a_L = \frac{{\rho V^2 A C_L}}{{2 m}}$$

At this point, we should know all acceleration vectors on the golf ball. These are:

• acceleration due to lift
• acceleration due to drag
• gravity

We need to translate all of these accelerations into x and y components. How do we do this?

Well, we know that the acceleration of the golf ball due to lift acts orthogonal to the path of the ball, and the acceleration due to drag acts in the same direction as the ball's path. It looks something like this

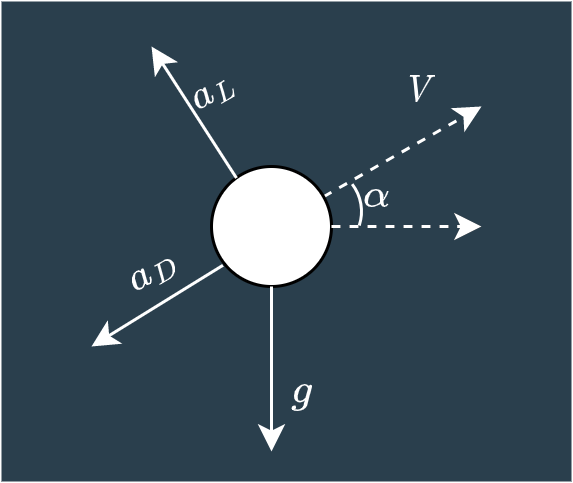
So, we have to perform a bit of trigonometry to transform these known acceleration vectors into the x, y plane like below.

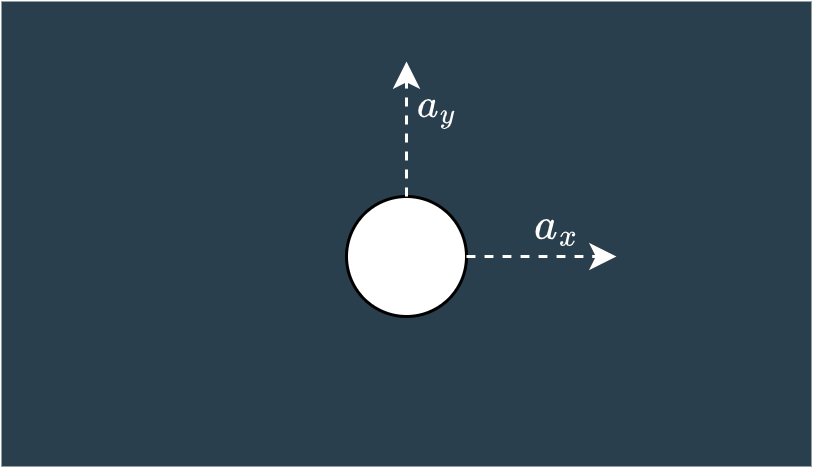
The translation is as follows

$$a_x = -a_D * \cos(\alpha) - a_L * \sin(\alpha) a_y = -a_D * \sin(\alpha) + a_L * \cos(\alpha) - g$$

At this point, we have accelerations in the xy plane, but we still don't know the values for lift and drag coefficients to solve for acceleration. This is where we need to turn to the research.

From the referenced aerodynamics research study, we can pull the following equations for drag and lift coefficients

Drag Coefficient

$$C_D = \begin{cases} 1.29 \times 10^{-10} \times \text{Re}^2 - 2.59 \times 10^{-5} \times \text{Re} + 1.50, & \text{if } \text{Re} < 10^5 \\ 1.91 \times 10^{-11} \times \text{Re}^2 - 5.40 \times 10^{-6} \times \text{Re} + 0.56, & \text{if } \text{Re} \geq 10^5 \end{cases}$$

Lift Coefficient

$$C_L = -3.25 * S^2 + 1.99 * S$$

Now that we understand the aerodynamics of the problem, we will set up the simulation in the next blog.